 |
Nachdem das Bild segmentiert wurde und weiterhin als Matrix vorliegt, gilt es, zusammenhängende Regionen zu finden und in einer platz- und damit rechenzeitsparenden Weise zu kodieren.
Während es verschiedene allgemeine Techniken der komprimierten Speicherung der Bilddaten gibt -- an dieser Stelle seien nur die Lauflängenkodierung und die Quad-Bäume genannt -- wird hier mit der Kettenkodierung eine umrißbeschreibende Kodierung gewählt. Während sie ähnlich wie die beiden anderen Techniken eine deutliche Komprimierung der Daten bei gleichzeitiger Erhaltung sämtlicher Informationen erzielen kann, werden bei ihr die eigentlich interessierenden Regionen explizit kodiert. Die Regionenkodierung eignet sich besonders, um schnell eine objektorientierte Beschreibung des Bildes zu etablieren, bei der die einzelnen Regionen im Mittelpunkt stehen.
 |
Die vorliegende Implementierung besteht im wesentlichen aus zwei Teilen. Ein Teil kümmert sich um das Abschreiten der von der Segmentierung erhaltenen Matrix von oben links nach unten rechts. Trifft die Schleife auf einen Punkt einer neuen Region, d.h. wechselt der Farbkode und ist dieser Punkt noch nicht als Randpixel markiert, stößt sie den zweiten Teil an. Der zweite Teil startet die Kodierung der Region. Die Koordinaten des Anfangspixels werden in einem neuen Regionenobjekt abgespeichert, anschließend die Kontur abgeschritten und der Kettenkode abgespeichert. Alle Pixel, die zur Regionenkontur gehören, werden als Konturpixel markiert, um zu verhindern, daß die gleiche Kontur zweimal untersucht wird.
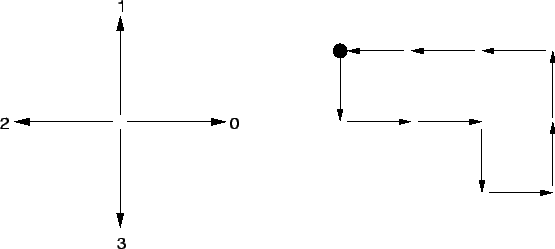
Die Konturverfolgung selbst ist hier als Strategie mit einem abstrakten Interface deklariert. Es liegen zwei verschiedene Strategieobjekte vor, eines für die Kodierung mittels 4er, das andere für die 8er Nachbarschaft. Die numerischen Kodes der Richtungen in der 4er Nachbarschaft werden mit 2 multipliziert, so daß die Kodierungen der Richtungen in beiden Nachbarschaftsarten übereinstimmen. Die Implementierung der äußeren Schleife wird bei der Instanzierung dann je nach Wunsch des Klienten mit einer der beiden Konturverfolgungsstrategien konfiguriert.
Der vorliegende Algorithmus kann auf Wunsch des Anwenders auch innere Regionen untersuchen. Standardmäßig bleiben sie aber unverarbeitet.
Alle gefundenen Regionen werden anhand ihrer Farbklasse gruppiert und so geordnet zurückgegeben.
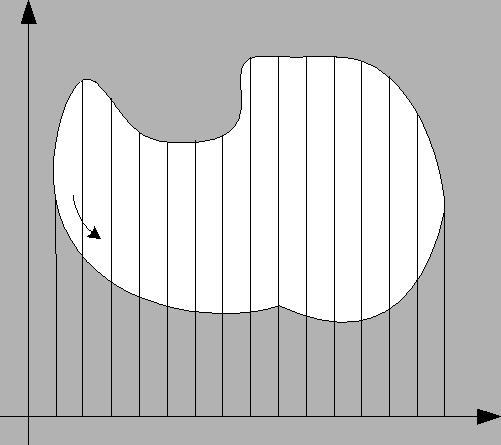
Ein Vorteil des Kettenkodes ist es, daß aus ihm wichtige Größen wie Fläche und geometrisches Zentrum mit geringem, bzgl. der Konturlänge linearen Rechenaufwand ermittelt werden können.
Dies geschieht durch Integrieren der oberen und unteren Objektkante. Die Differenz dieser beiden Integrale ist nun genau die Objektfläche (Abbildung 2.8). Da es sich bei den Kettenkodes um diskrete Schritte handelt, ist Integrieren einfaches Summieren. Beide Summen können durch einmaliges Abschreiten des Kettenkodes ermittelt werden. Wird der Koordinatenursprung auf den Startpunkt des Kettenkodes gesetzt und merkt man sich die Höhe des aktuellen Konturpunktes, gilt es, bei einem Linksschritt die Höhe zur Summe der oberen Kante und bei einem Rechtsschritt zur Summe der unteren Kante zu addieren.
 |
Eine genaue Beschreibung des Algorithmus zur Berechnung der Fläche findet man zum Beispiel bei Sonka et al. [19]. Die Berechnung des Schwerpunktes läßt sich aus diesem Algorithmus so entwickeln, daß er ähnlich einfach berechnet werden kann.