Zum Training wird hier ein Clustering-Algorithmus verwendet. Und zwar handelt es sich um eine Generalisierung des k-means Algorithmus [11] für Klassifizierungszwecke.
Beim Clustern werden im allgemeinen repräsentative Vektoren für eine Menge
von multidimensionalen Datenvektoren
gesucht. Die Vektoren sind in folgendem Sinne repräsentativ: Seien ![]() Vektoren
Vektoren
![]() in einem
in einem ![]() -dimensionalen Raum gegeben. Dann
partitioniert eine Menge von
-dimensionalen Raum gegeben. Dann
partitioniert eine Menge von ![]() Zentren
Zentren
![]() die Daten
die Daten ![]() in
in
![]() Mengen
Mengen
![]()
![]() , wobei jede Menge
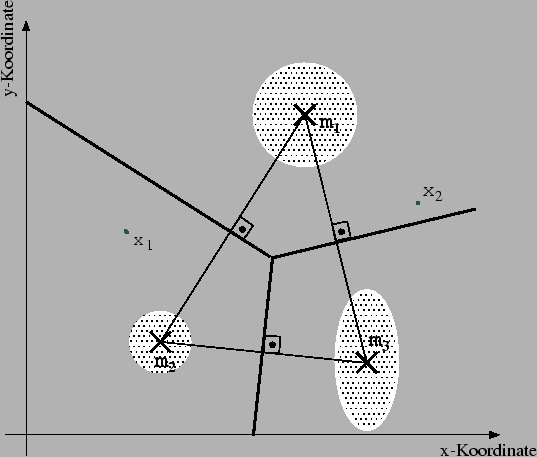
, wobei jede Menge ![]() die Punkte aus X beinhaltet, die innerhalb des
Voronoi Polyeders des Zentrums
die Punkte aus X beinhaltet, die innerhalb des
Voronoi Polyeders des Zentrums ![]() liegen:
liegen:
| (26) |
|
Der k-means Algorithmus findet iterativ eine lokal-optimale Menge von ![]() Zentren, ausgehend von einer Menge
Zentren, ausgehend von einer Menge ![]() von
von ![]() zufällig positionierten
Zentren, mit Hilfe der Anpassungsregel:
zufällig positionierten
Zentren, mit Hilfe der Anpassungsregel:
| (28) |
Um nun diesen Algorithmus für die vorliegende Klassifizierungsaufgabe zu
verwenden, werden zusätzlich Klassen eingeführt. Hierbei erhält jeder
Datenvektor ![]() eine Klasse
eine Klasse
![]() zugeordnet. Nun
werden für jede einzelne Klasse
zugeordnet. Nun
werden für jede einzelne Klasse ![]()
![]() optimale Zentren
optimale Zentren
![]() gesucht Die Menge der im
Voronoi-Polyeder liegenden Datenpunkte und die zugehörige, in Regel
(3.3) benötigte Indikatorfunktion müssen dabei
folgendermaßen angepaßt werden:
gesucht Die Menge der im
Voronoi-Polyeder liegenden Datenpunkte und die zugehörige, in Regel
(3.3) benötigte Indikatorfunktion müssen dabei
folgendermaßen angepaßt werden:
| (29) |
| (30) |
Dieser Algorithmus hat aber zwei wesentliche Probleme beim Finden von Klassengrenzen: Zum einen befinden sich relativ viele Zentren in der Mitte der Klassen, obwohl nur die Zentren am Rand der Cluster die Grenzen und damit die Klassifizierung bestimmen. Schlimmer wiegt aber noch das Initialisierungsproblem. Es ist nicht bekannt, wieviele Zentren jeder Klasse für eine gute Klassifizierung benötigt werden und wo sie positioniert werden müssen.
Diesen Problemen wird mit einer Erweiterung der Zustandsbeschreibungen der
Zentren begegnet, wie es von Marroquin und Girosi beschrieben wird
[11]. Neben der Position eines Zentrums werden zusätzlich Daten über
das dynamische Verhalten in die Zustandsbeschreibung aufgenommen. Zum einen
wird die Anzahl der Datenpunkte innerhalb des Voronoi-Polyeders unabhängig von
der Klassenzugehörigkeit gezählt (Gleichung 3.7), zum anderen nur
solche Datenpunkte gleicher
Klasse (Gleichung 3.8). Ein erweiterter Zustand ist
dann
![]() mit
mit
Anhand dieser Daten, wie oft ein Zentrum über die anderen Zentren gewonnen hat
und wie viele der Datenpunkte in seinem Einflußbereich die gleiche Klasse
haben, kann die Zahl der Zentren dynamisch angepaßt werden. Es wird mit einer
beliebigen Menge Zentren beliebiger Klasse gestartet. Prinzipiell ist es auch
möglich, wenn man eine längere Laufzeit in Kauf nimmt, mit nur einem einzigen
Zentrum zu beginnen. Anschließend wird nach jeder Iteration des k-means
Algorithmus jedes Zentrum ![]() nach der ersten zutreffenden der folgenden
Regeln angepaßt:
nach der ersten zutreffenden der folgenden
Regeln angepaßt:
Nachdem die Parameter ![]() ,
, ![]() und
und ![]() bei der Implementierung des Algorithmus entsprechend angepaßt wurden, zeigt
dieses Training eine sehr gute Konvergenz innerhalb weniger Iterationen. Dem
Benutzer wird damit ein Werkzeug zur Verfügung gestellt, mit dem er das System
innerhalb weniger Sekunden auf neue Lichtverhältnisse oder neue Farbmarker
einrichten kann. Bei den vorgenommenen Tests erweist sich das Training im
UV-Raum gegenüber wechselnden Lichtverhältnissen als wesentlich robuster. Es
lassen sich ohne großes ``Herumspielen'' Segmentierungen mit erstaunlich
niedrigen Fehlern trainieren. Um den Benutzer ein wenig in das
Trainings- und Generalisierungsverhalten eingreifen zu lassen, kann er die
durchschnittliche Anzahl der Zentren pro Klasse mit Hilfe eines Schiebereglers
anpassen. Je nach Stellung werden
bei der Implementierung des Algorithmus entsprechend angepaßt wurden, zeigt
dieses Training eine sehr gute Konvergenz innerhalb weniger Iterationen. Dem
Benutzer wird damit ein Werkzeug zur Verfügung gestellt, mit dem er das System
innerhalb weniger Sekunden auf neue Lichtverhältnisse oder neue Farbmarker
einrichten kann. Bei den vorgenommenen Tests erweist sich das Training im
UV-Raum gegenüber wechselnden Lichtverhältnissen als wesentlich robuster. Es
lassen sich ohne großes ``Herumspielen'' Segmentierungen mit erstaunlich
niedrigen Fehlern trainieren. Um den Benutzer ein wenig in das
Trainings- und Generalisierungsverhalten eingreifen zu lassen, kann er die
durchschnittliche Anzahl der Zentren pro Klasse mit Hilfe eines Schiebereglers
anpassen. Je nach Stellung werden ![]() und
und ![]() um den gleichen
Faktor erhöht oder erniedrigt.
um den gleichen
Faktor erhöht oder erniedrigt.