Objektgeschichte

Für die Bestimmung der Geschwindigkeit und zur Aufzeichnung von objektbezogenen Daten über einen längeren Zeitraum gilt es, eine Korrespondenz zwischen den Objekten aufeinanderfolgender Einzelbilder zu etablieren. Können die Objekte nicht anhand eindeutiger Merkmale differenziert werden, gestaltet sich die Zuordnung als nicht triviales Problem. In einem solchen Fall hat man eine Menge von ununterscheidbaren Objekten gleichen Typs in einem Bild und eine Menge mit Objekten im aktuellen Bild gefunden. Hierbei bezeichne die Position des -ten Objektes aus . Nun gilt es, Beziehungen zwischen den Objekten dieser beiden Mengen herzustellen. Wenn dies eben nicht anhand der äußeren Merkmale geschehen kann, gilt es die Bewegungen an sich zu analysieren (Abbildung 2.10). Aufgrund der schon erläuterten Möglichkeit der unvollständigen Pfade muß nicht zwingend gelten und jedes Objekt der einen Menge einen Nachfolger bzw. Vorgänger in der anderen Menge besitzen.

Abbildung 2.10: Segmentierung zweier aufeinanderfolgender Einzelbilder. Es ist nicht feststellbar, welches der beiden Objekte sich nach oben und welches sich nach unten bewegt hat. Diese Zuordnung kann nur anhand der gesamten Bewegung vollzogen werden.

Um die Zuordnungen zu finden, wird häufig eine Kostenfunktion definiert und anschließend minimiert. Meistens werden die möglichen Zuordnungen anhand von einfachen physikalischen Grundmodellen bewertet. Die Minimierung wird oftmals durch die Formulierung als Suchproblem und durch einen hoch spezialisierten Suchalgorithmus realisiert. Domänenwissen wird hierbei nicht nur zur Erstellung der Modelle herangezogen, sondern auch bei der Auswahl und Optimierung der Suchmethoden. Sethi und Jain [18] schlagen zum Beispiel ein Modell vor, daß gleichmäßige Bewegungen bevorzugt. Rangarajan und Shah [12] schlagen mit dem ``proximal uniformity'' Modell hingegen kleine Bewegungen und konstante Geschwindigkeit als Kriterien vor.

Viele der diskutierten Lösungen haben aber Probleme bei unvollständigen Pfaden. Während eine Lösung an Verdeckungen scheitert, hat die andere Probleme mit Aus- oder Wiedereintritten [16], [3]. Generell gestalten sich die allgemeinen Lösungen derzeitig als nicht schnell genug, um viele Objekte auf engem Raum in Echtzeit zu verfolgen. Deshalb kann hier keine allgemeine Lösung, die unter allen Bedingungen die geforderte Robustheit bei gleichzeitiger Echtzeitverarbeitung garantiert, formuliert werden.

Vielmehr wird hier ein einfacher, für die Problemstellung und die Benchmarks optimierter Algorithmus implementiert. Hierbei wurden bezüglich unvollständiger Pfade einige den Algorithmus vereinfachende Annahmen aufgestellt:

1. Ein- und Austritte treten nur einzeln auf. Wenn gilt, sind Objekte ausgetreten. Gilt , sind Objekte eingetreten, gilt hingegen , liegen weder Ein- noch Austritte vor. Diese Annahme ist nicht nur in Umgebungen, wo Ein- und Austritte nur selten auftreten, plausibel, sondern ist wohl auch mit einer hohen Wahrscheinlichkeit ganz allgemein korrekt, wenn man eine hohe Bildrate und relativ wenige Objekte voraussetzt.
2. Ein einmal ausgetretenes Objekt tritt nicht wieder ein. Das bedeutet, daß die ID eines ausgetretenen Objektes nicht wieder vergeben wird. Das Unterscheiden von Ein- und Wiedereintritten spielt für die Bestimmung der Geschwindigkeit wie auch für reaktive Agenten keine Rolle. Sollte die Entdeckung z.B. für die Generierung von Steuerbefehlen benötigt werden, muß ein Wiedereintritt in einer höheren Verarbeitungsschicht festgestellt werden.

Bevor der aufwendige Matching-Algorithmus selbst angeworfen wird, werden zuerst alle Objektklassen untersucht und die Fälle aussortiert, für die eine Zuordnung ad hoc möglich ist. Eine Zuordnung kann in folgenden Fällen direkt vorgenommen werden:

n=0

Es wurden im aktuellen Bild keine Objekte gefunden. Alle Objekte der Menge werden entweder anhand eines linearen Modells fortgeschrieben oder gelöscht.

m=0

Alle Objekte sind neu eingetreten und erhalten daher eine neue Identifizierungsnummer und eine leere Geschichte.

m=n=1

Das einzige Objekt in kann direkt dem einzigen Objekt in zugeordnet werden.

Zum Finden der Zuordnung wird hier eine Uniform-Cost-Suche verwendet [15]. In jeder Ebene des Suchbaumes wird eine Zuordnung mehr vorgenommen. Dabei werden nacheinander den Objekten der Menge alle Objekte der Menge zugeordnet. Die Suche beginnt also mit einem Knoten, in dem noch keine Zuordnungen getroffen wurden. Wird dieser Knoten expandiert, werden dem ersten Objekt aus in neuen Knoten alle Objekte aus zugeordnet. Wird wiederum einer dieser neuen Knoten expandiert, werden nun in neuen Knoten dem zweiten Objekt aus alle in verbliebenen Objekte zugeordnet. Ein Sonderfall ergibt sich beim Expandieren, wenn gilt. In einem solchen Fall bleiben Elemente einer Menge unzugeordnet. Dies wird beim Aufspannen berücksichtigt, indem, falls gilt, ein Knoten angelegt wird, bei dem das aktuell zuzuordnende Objekt aus explizit als unzugeordnet gespeichert wird. Die Reihenfolge, in der der Suchbaum durchlaufen wird, wird bei der Uniform Cost Search anhand einer Kostenfunktion bestimmt. Die Söhne des ``billigsten'' Knotens werden zuerst untersucht. Die Kostenfunktion bewertet die getroffenen Zuordnungen eines Knotens nach physikalischen Gesichtspunkten. Die Uniform-Cost Search ist hierbei vollständig und optimal, d.h. es wird in jedem Fall die günstigste Zuordnung, also hier die Zuordnung mit dem geringsten Abstand aller Objekte, gefunden.

Abbildung 2.11: UML-Diagramm der Komponente ``allgemeinen Suchshell''

Abbildung 2.12: Allgemeiner Suchalgorithmus nach Russell und Norvig.

Hier wurde nun diese Suchshell unter Verwendung abstrakter Datentypen in einem objektorientierten Ansatz implementiert (Abbildung 2.11). Die Komponente besteht aus einer Reihe von abstrakten Interfaces und problemunabhängigen Implementationen. Wie in der Vorgabe von Russel und Norvig galt es, die allgemeinen Suchalgorithmen sauber von den zu lösenden Problemen zu trennen. Auf der höchsten Ebene bilden die Klassen CProblemState und CProblemSolvingStrategy abstrakte Interfaces zu Problemlösungsalgorithmen. Während CProblemState eine völlig leere Deklaration ist und die problemabhängigen Daten kapselt, wird in CProblemSolvingStrategy eine Methode deklariert, die bei der Übergabe eines Anfangszustandes eine Lösung zurückliefert.

In der nächsten Ebene wird nun die allgemeine Suchshell nach R&N definiert. CGoalTestStrategy, CExpandStrategy sind abstrakte Deklarationen von Strategieobjekten, die den Goal-Test und die Expandierungsstrategie nach R&N bereitstellen. Während bei R&N in einem funktionalen Ansatz eine Queueing-Funktion und eine Liste von Knoten verwendet wird, wurde hier ein abstrakter Datentyp CProblemStateQueue deklariert. Wie der Name schon andeutet, handelt es sich um eine einfache Schlange. Um nun eine spezielle Einordnung zu erreichen, müssen die enqueue Methoden entsprechend implementiert werden. Mit diesen drei Strategien wird die Suchstrategie konfiguriert. Die Klasse CSearchStrategy implementiert hier das Interface CProblemSolvingStrategy mit der allgemeinen Suchshell. Diese Klasse ist die Grundlage aller Suchalgorithmen. Die Methode solve enthält nun eine direkte Umsetzung des Algorithmus von R&Ns allgemeiner Suchshell:

CProblemState* 
CSearchStrategy::solve(CProblemState* problem)
{
  vector<CProblemState*> expanded;
  stateQueue->clear();
  stateQueue->enqueue(problem);      
  
  while(true) {                  
    if (stateQueue->isEmpty())       
      return 0;

    problem=stateQueue->dequeue();   

    if (goalTestStrat->isGoal(problem))
      return problem;
                           
    expandStrat->expand(problem, &expanded);
    stateQueue->enqueue(expanded);      
    expanded.clear();                    
  }
  return 0;
}

In der nächsten Ebene werden die Hilfsklassen für die Suchtypen spezialisiert, die Kostenfunktionen oder Heuristiken verwenden. Hierzu wird vom Interface CProblemState ein weiteres Interface für bewertete Problemzustände abgeleitet. CEvaluatedProblemState besitzt ein Attribut cost, in dem die Kosten des enthaltenen Zustandes oder die Bewertung der Heuristik abgespeichert werden können. Außerdem wird ein Interface für eine solche Evaluierungsstrategie deklariert. Die Zustandsschlange wird um eine Konfigurationsmöglichkeit mit einer solchen Evaluierungsstrategie erweitert. Die Implementierung der Einordnungsmethode enqueue verwendet die Bewertungsstrategie dann zum Einordnen der neuen Zustände.

In einer weiteren Ebene wird noch eine Evaluierungsstratgeie definiert, die aus einer Komposition zweier einfacher Evaluierungsstrategien besteht. Die Kosten beider Strategien werden einfach addiert. Eine solche Komposition wird zum Beispiel vom Algorithmus verwendet, der eine Kostenfunktion des bisherigen Pfades und eine Heuristik für die Kosten des noch bis zum Ziel abzuschreitenden Pfades verwendet. Auch das Aufspalten einer komplizierten Funktion ist so möglich. Dabei kann eine aus Objektkomposition entstandene Evaluierungsstrategie zur Laufzeit auch in einer weiteren Komposition verwendet werden.

In der untersten Ebene des UML-Diagramms sieht man nun die implementierenden Klassen der problemunabhängigen Teile der Interfaces. Da in dieser Bibliothek eine Uniform-Cost-Suche verwendet wird, wird eine CEvaluatedProblemStateQueue implementiert. Anstatt einen solchen Datentyp von Grund auf neu zu implementieren, wird die in der Standard Template Library von C++ enthaltene Priority Queue, eine Schlange, bei der Elemente anhand einer Priorität angeordnet werden, für die Suche adaptiert.

Durch diese saubere, modulare Anlage der Suchalgorithmen wird eine durch Implementierung einiger Interfaces einfach anpassbare und um weitere Suchalgorithmen erweiterbare Komponente geschaffen.

Abbildung: UML-Diagramm der problemspezifischen Implementierungen mit den zugehörigen abstrakten Interfaces der Suchshell.

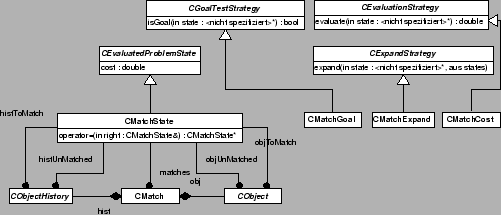Nun gilt es, diese Suche für das hier vorliegende, konkrete Matching Problem anzupassen, indem die Interfaces wie in Abbildung 2.13 implementiert werden. Ein Zustand, bzw. Knoten des Suchbaumes, in CMatchState enthält alle bereits getroffenen Zuordnungen (Hilfsklasse CMatch), je eine Liste aller noch zuzuordnender Objektgeschichten und Objekte und zwei Listen mit den Objekten und Objektgeschichten, die keinen Partner haben (Ein- oder Austritt). Hier werden also nicht nur die Objekte des Bildes denen des Bildes zugeordnet, sondern auch die Objekte des Bildes in eine Objektgeschichte der letzten Einzelbilder eingeordnet.

Wird nun von der Matching Schicht eine Suche benötigt, gilt es, einen Anfangszustand aus den detektierten Objekten und den Objektgeschichten aus dem letzten Einzelbild herzustellen. Hierzu werden einfach alle Objekte und Geschichten in die Liste der noch zuzuordnenden Objekte und Geschichten eingefügt. Mit diesem Anfangszustand wird dann die Suche gestartet. Anschließend müssen aus der Lösung die Zuordnungen ausgelesen und vorgenommen werden. Objekten, denen keine Geschichte zugeordnet wurde, erhalten eine neue Objektgeschichte, Objektgeschichten, denen kein Objekt zugeordnet wurde, müssen entweder anhand eines Modells fortgeschrieben oder gelöscht werden.

Im Ergebnis dieser Schicht liegt dann eine Gruppierung der Objektgeschichten nach ihrem Typ vor. Jede dieser Objektgeschichten besitzt eine eindeutige ID.

• Kostenfunktionen