Kostenfunktionen

Für die Bewertung der Zuordnungen wird eine Kostenfunktion benötigt. Eine mitgelieferte Kostenfunktion verwendet den Euklidschen Abstand zweier Punkte als Maß. Bei Verwendung dieser einfachen aber schnell zu berechnenden Kostenfunktion wird jeder Punkt aus der zum Zeitpunkt

aufgenommenen Szene seinem nächsten Nachbarn in der Szene des aktuellen Zeitpunkts

zugeordnet. Diese Zuordnung ist aber offensichtlich nur bei langsamen Bewegungen und einer geringen Punktdichte sinnvoll.

Für anspruchsvollere Domänen, bei denen viele, sich schnell bewegende Punkte auftreten, wird eine komplexere Kostenfunktion benötigt. Salari und Sethi schlugen schon 1987 eine Kostenfunktion vor, die sowohl gleichmäßige Bewegungen (geringe Richtungsänderungen) als auch konstante Geschwindigkeiten bevorzugt [18]. Diese Kostenfunktion stellt den Standard im Bereich des Feature-Point-Tracking dar und ist sehr gut für das Pendelproblem geeignet, weil sie keine Probleme mit sich überkreuzenden Pfaden hat. Um Geschwindigkeits- und Richtungsänderungen bewerten zu können, benötigt sie nicht nur die aktuelle und letzte, sondern auch die vorletzte Position:

		$\displaystyle \delta(\vec{p}_{t-2,i}, \vec{p}_{t-1,j}, \vec{p}_{t,k})=$	(22)
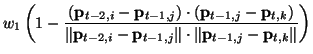		$\displaystyle w_1 \left( 1- \frac{(\vec{p}_{t-2,i}-\vec{p}_{t-1,j})\cdot(\vec{p... ...2,i}-\vec{p}_{t-1,j}\Vert\cdot\Vert\vec{p}_{t-1,j}- \vec{p}_{t,k}\Vert} \right)$
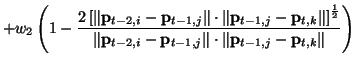		$\displaystyle +w_2\left(1- \frac{2\left[\Vert\vec{p}_{t-2,i}-\vec{p}_{t-1,j}\Ve... ...2,i}-\vec{p}_{t-1,j}\Vert\cdot\Vert\vec{p}_{t-1,j}- \vec{p}_{t,k}\Vert} \right)$

Der Bruch im ersten Term berechnet den Cosinus des Winkels $\gamma$ bezüglich der beiden Richtungsvektoren. $\cos \gamma$ ist gleich 0, wenn die Vektoren senkrecht zueinander stehen, und 1, wenn sie parallel sind. Der gesamte erste Term bestraft damit Richtungsänderungen.

**Abbildung:** Zweiter Term der Fehlerfunktion nach Sethi und Jain. Die Kosten beziehen sich auf das Längenverhältnis der beiden Strecken, wobei die feste Länge der ersten Strecke und die variable Länge der zweiten Strecke bezeichnet. Im Falle $\frac{b}{a}=1$ sind die Strecken gleich lang und die Kosten damit gleich Null.
$\resizebox {1\columnwidth}{!}{\includegraphics{GraphVel.eps}}$

Die Gewichte

und

werden zum Gewichten der beiden Komponenten der Kostenfunktionen verwendet. Üblich ist dabei die Gewichtung

und

([18], [16], [3]). Dieses Verhältnis muß aber an die jeweilige Situation angepaßt werden.

Die Kostenfunktion ist außerdem normiert: Es gilt $0\leq \delta(\vec{p}_1, \vec{p}_2, \vec{p}_3) \leq 1$ für alle $\vec{p}_1, \vec{p}_2, \vec{p}_3$ aus $\textbf{R} \times \textbf{R}$ .